Crafting mechanism design
by Harang Ju, Akhil Jindal, Madhav Kumar
Table of contents
- Overview
- Crafting events
- Models of crafting
- Crafting usage
- Individual usage
- Value burned
- Discussion
- Code and data
- References
Overview
Tokens are a fundamental medium of value in web3, especially in gamified blockchain experiences. Emissions of tokens—from fungible “coins” to non-fungible items and characters—are essential to expand the supply or variety of tokens for a growing population of users.
To support token value, token supply can be balanced by allowing users to craft desirable digital items using existing tokens, both fungible and non-fungible alike. However, it is unexplored how the design of crafting mechanisms influence users’ crafting behavior. In this paper, we explore two crafting events, Lunacian Express (LE) and Lunacian Summer (LS) in the blockchain game Axie Infinity [1,2].
We find that using any, versus special, items to craft increases the number of participants, but sequential crafting of rarer and rarer items increases the individual usage. We frame these events using two models—parallel versus sequential—each with contrasting properties.
We suggest that a system designer airdrop NFTs to users to maximize participation and design sequential crafting of rarer items to maximize retention.
Crafting events
Blockchain games offer the opportunity to explore users’ economic behavior because economic activity is public on a blockchain. An interesting economic activity is crafting, in which a user consumes resources to obtain an item [3]. Here, we refer to all non-fungible tokens as items, whether they are called items, characters, or land in their respective platforms. Thus, we consider breeding—i.e., using characters and resources to craft additional characters—as a type of crafting.
In this case study, we explore two crafting events in the blockchain game Axie Infinity: Lunacian Express and Lunacian Summer. While the crafting mechanisms differ across many parameters in the two events, this exploration reveals insights into how the design of crafting mechanisms may affect crafting usage behaviors.
Models of crafting
We present two, non-exclusive mechanisms of crafting items of differing rarity (Figure 1). These two mechanisms model the two crafting events we study here, respectively. In parallel crafting, one crafting action leads to multiple rarities with corresponding probabilities, as in gacha games. Thus to obtain rare items, a user must craft multiple times. In sequential crafting, a user must craft with the crafted materials to obtain rarer and rarer items [4].
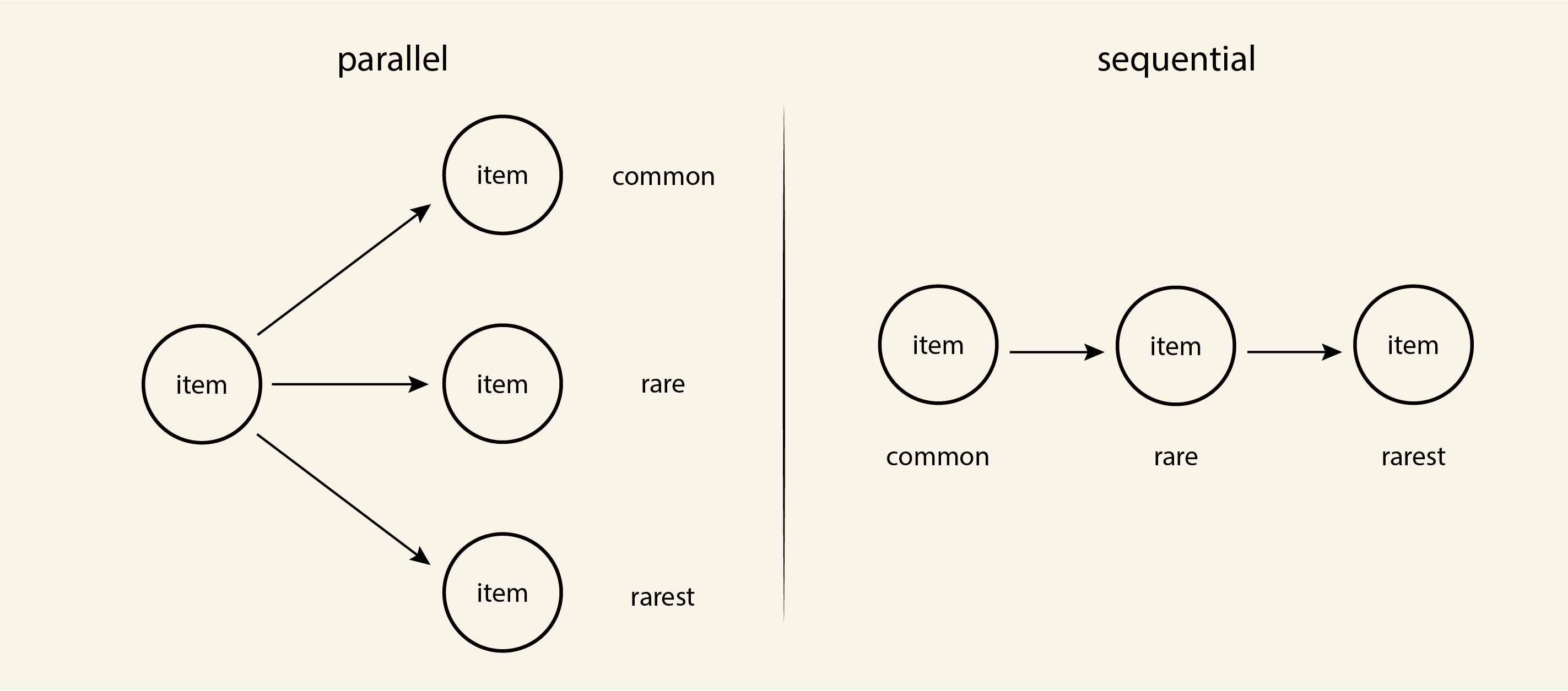
We hypothesized that parallel crafting is better for increasing the number of participants due to its simplicity and sequential crafting better for individual usage due to its dependence on time and the crafting process. We categorize the Lunacian Express as mostly a parallel craft and the Lunacian Summer as mostly a sequential craft, though there are elements of both types of crafting in both events (the two models are not mutually exclusive; Figure 2).
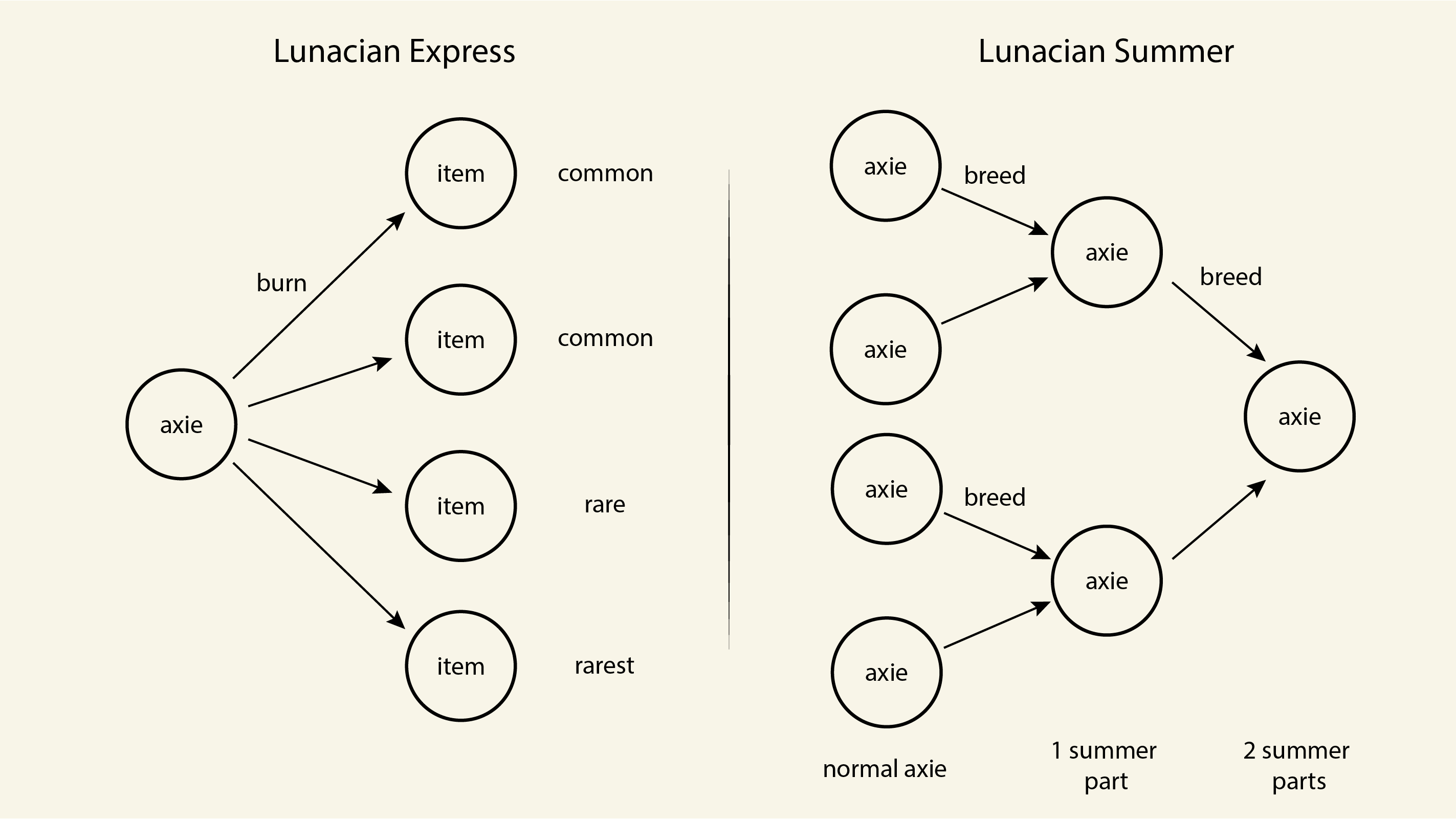
Lunacian Express was a 31-day crafting event during which a user can burn a playable character, called an axie, in exchange for Lunar New Year-themed items (Figure 3). In the process of burning, an axie is sent to an address, where the original owner no longer owns the axie. In exchange, the user immediately receives one of five items with differing probabilities: 35%, 35%, 20%, 9%, and 1% for each of the five items. Additionally, participants enter a raffle for even rarer items. The user can claim the items at the end of the event.
Lunacian Summer was a 50-day long breeding event during which a user can breed axies with certain body parts to create an axie with a summer-themed part (Figure 4). Summer-themed axies can then also be bred together to pass on summer-themed parts to their child axies, thus creating axies with more summer parts which become rarer. Further, when each summer skin is bred, there is a 1% chance for it to be a shiny part, which is not inheritable.

Crafting usage
The two crafting events, Lunacian Express and Lunacian Summer, produced starkly contrasting usage patterns (Figure 5). In LE, most usage occurs in the first few days of the event, with relatively little usage through the rest of the event, apart from a small increase in usage near the end of the event. In LS, breeding is cyclic with a period of five days, which is the incubation time between breeding and morphing the axie egg into an adult axie. Usage falls during the event but far less than in LE.
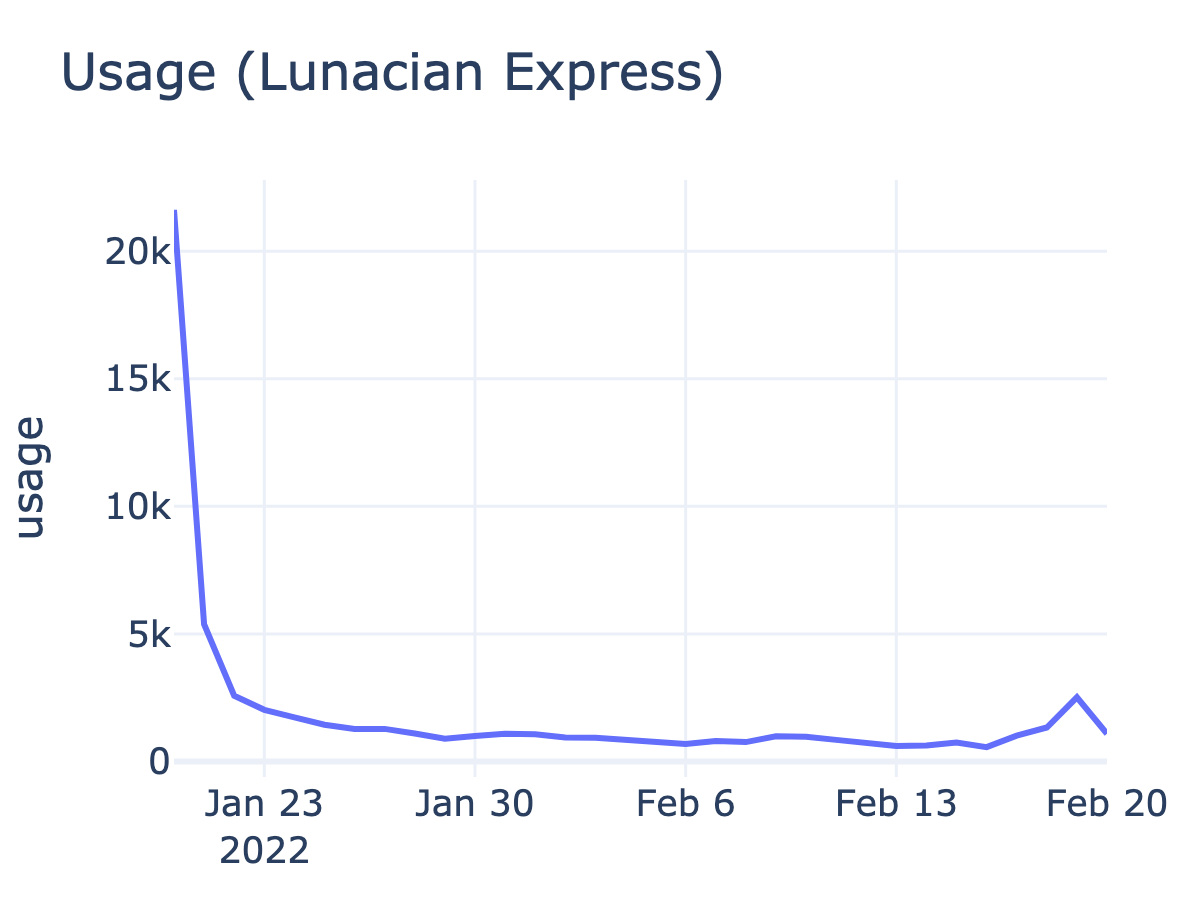
Despite the precipitous drop in usage for Lunacian Express, usage is still an order of magnitude higher than in Lunacian Summer. The peak daily usage is 21,618 for LE and 3,158 for LS. Total usage is 147,456 for LE and 53,483 for LS.
The higher usage of Lunacian Express may be due to the design of Lunacian Express versus Lunacian Summer. In LE, any axie could be burned for the event, allowing any user with an axie to participate. In LS, only axies with certain parts could be used for the event (Figure 4). Accordingly, obtaining the requisite axies to participate in LS served as a barrier to entry for user participation and thereby decreased usage. For reference, there were 10,914,903 axies at the start of LE and 11,354,511 at the start of LS.
Note that the numbers for Lunacian Summer are for successful breeds only. Computing the numbers for all attempts at summer axies are computationally intensive, as we need to search all axies bred during the event. However, only two parts have less than 100% probability of success, vanilla ice cream and turtle buoy (both with a 13% chance), and they only constitute a small fraction of axies bred during the first breeding cycle, at 1.4% and 1.3%, respectively.
Individual usage
The two crafting events, Lunacian Express and Lunacian Summer, produced contrasting individual usage distributions (i.e., how many times a user burned an axie in LE or bred an axie in LS). Both events have more users who craft a large number of items than one would expect in an exponential usage distribution.
Mathematically, the usage distributions follow a power law: \(f(x) = x^{-\alpha}\). A power law is observed in many natural and human phenomena and is often called the Pareto distribution or, in some cases, the 80-20 rule [5]. The distribution has a heavy tail, with more rare events than in exponential distributions, and is scale-free, which produces a straight line on a log-log plot.
Interestingly, power law distributions are produced by a class of mechanisms different from those that produce exponential distributions. In an exponential distribution, the more one does something, the harder it is to do that thing. For example, the more one flips a coin, the harder it is to get all heads or all tails. However, in a power law distribution, the more one does something, the easier it is to do that thing. The Lindy effect is one famous example among the NFT community for having such property [6].
The usage distribution of LE has a power law exponent \(\alpha\) of 2.3, and that of LS has \(\alpha\) of 1.7 (Figure 6). Thus, at face value, far more people had higher usage in LS than in LE (\(KS = 0.30\), \(p \ll 0.001\)).
Mathematically, the usage distribution of LE has no defined variance, with \(\alpha < 3\), and that of LS has no defined average value, with \(\alpha < 2\). Thus, if the LS event never ended, the users would theoretically keep breeding summer axies. Further, common statistics, such as averages and variances, may not apply to this type of data.
The mathematical properties prompt design questions appropriate for a heavy-tailed distribution. For example, how does a designer capture the most value from the users at the tail of the distribution? How can a designer change the crafting process to incentivize users to the tail of the distribution?
Daily usage distributions reveal even further about user behaviors (Figure 7). In LS, far fewer users only breed once daily than in LE (\(\alpha_{LS} = 2.2\), \(\alpha_{LE} = 2.4\)). In the rest of the distribution, more users have higher daily usage in LS than in LE (\(KS = 0.34\), \(p \ll 0.001\)). Thus, the crafting design may even affect daily usage behaviors.
Value burned
As an economic imperative, a game developer has to capture value from in-game activity, such as crafting. A key economic metric for in-game economies is the value burned in crafting. The value burned is the opportunity cost of using the token for crafting, whose alternative is to sell the token on the market. For each event, we estimated the value of tokens burned, both fungible and non-fungible.
In Lunacian Express, we estimated the value burned by using the daily floor price of axies throughout the event and multiplying by the daily number of axies burned. In Lunacian Summer, we estimated the value burned by using the SLP and AXS burned for all summer axies bred. The calculation does not account for the depreciation in axie value as an axie is bred; an axie can breed a total of 7 times, and each subsequent breed costs more in SLP but the same in AXS.
Although Lunacian Summer had more high-usage participants, Lunacian Express burned far more value (~4.2 times more), particularly at the start of the event. LE users burned axies worth around $7,917,952.66, and LS users burned SLP and AXS worth around $1,900,178.03.
The patterns in value burned are distinct between the two events. LE users burned most of the value at the start of the event, but LS users burned similar amounts of value throughout the event. A factor for the difference may be due to the crafting design. In the sequential crafting model, a user has to iteratively craft rarer and rarer items that are harder and harder to obtain.
One example of the increasing crafting difficulty is observed in the rising average amount of SLP used per breed during the event (Figure 9). To breed axies with more and more summer parts (for a maximum of 6), a breeder has to breed with the summer axies bred in previous breeding cycles. Because a breeder is left with fewer and fewer summer axies further along in the process of breeding axies with 6 summer parts, the breeder has to breed more with each axie, which cost more SLP.
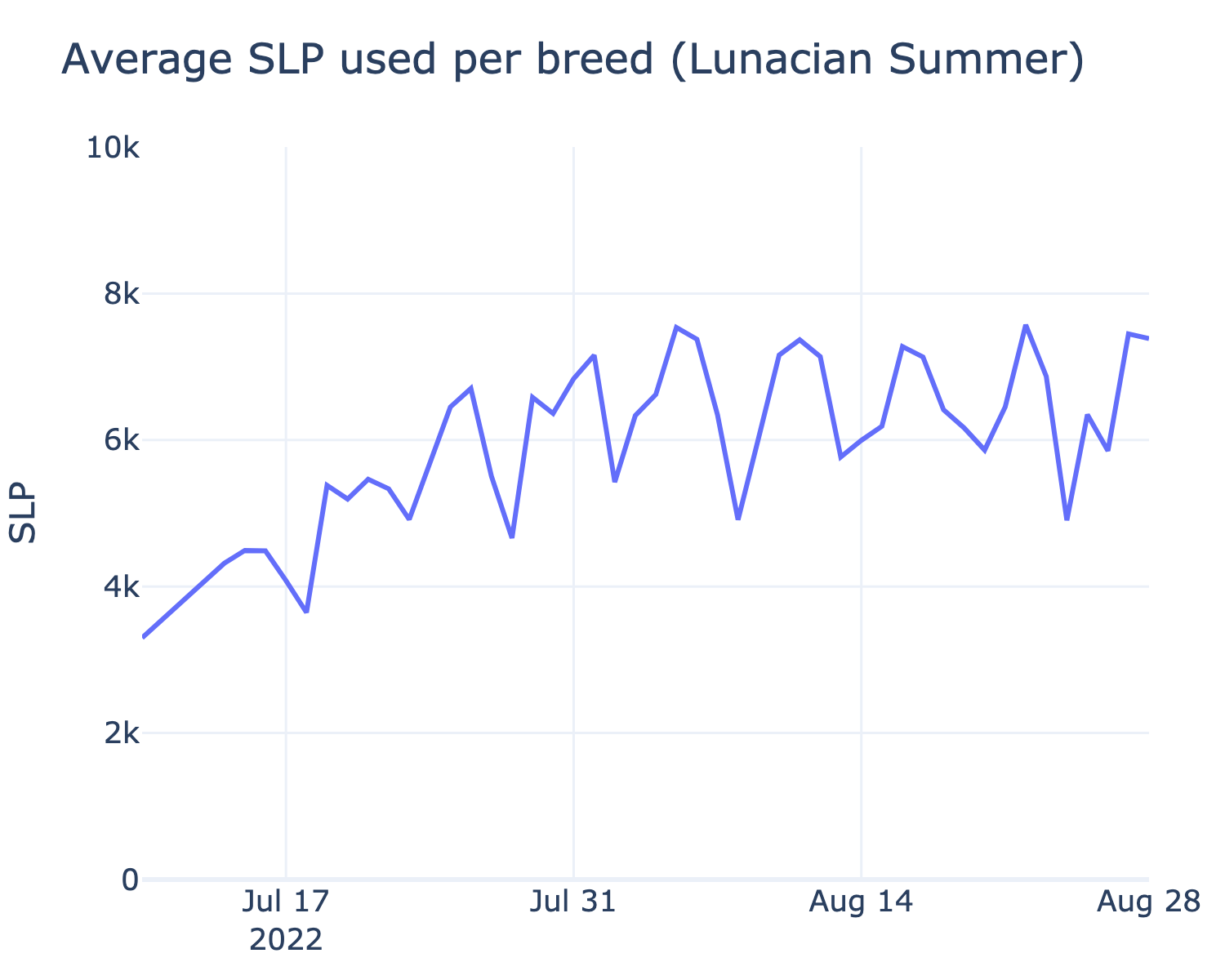
These results prompt interesting questions for game designers. Can one design a crafting mechanism to capture the best of both models and maximize the value of tokens burned? Can the design incentivize many users to participate at the start and then to keep burning tokens through the event? How can games reward and capture value from high-usage participants?
Discussion
This paper was a case study into crafting events in the blockchain game, Axie Infinity. By quantifying crafting usage in both events, we infer properties about the processes underlying the crafting mechanisms that may affect gross user behavior. Given insights into crafting mechanism design, a designer can choose to design for certain behaviors in the users and even target certain users (e.g., high-usage participants).
Our goal is not to argue for one model or another but to begin to reveal the relationship between crafting mechanism design and user behaviors. For example, not all crafting events should maximize for token value burned. In a limited-edition crafting event, perhaps the game designers want the users to produce a small number of collectibles that may have historical value in the future. In that case, a designer may optimize for secondary market volume instead of event participation.
Further studies are required to infer a causal relationship between the design of crafting mechanisms and usage. Without experiments, self-selection bias or other biases may influence the results. Thus in future studies, we aim to experimentally test crafting mechanisms on users to affect social and economic metrics.
Further, we demonstrate that we can use methods from other fields, such as statistical mechanics in this paper, to reveal user behaviors in the new blockchain economy. Such methods can be further strengthened by social analytics and experimentation. Moreover, these principles are generalizable to blockchain economies beyond those in games.
Finally, our findings suggest that to increase user participation, the tokens for crafting should be available to all potential users. One way to ensure that the availability of the tokens is to airdrop the token to all potential users. Then, to increase user retention and high usage, each crafting step should use tokens available in previous steps and incentivize the step by crafting rarer or more items. The nascent free-to-own model is one model that encapsulates these incentive structures. (Disclaimer: I own free-to-own DigiDaigaku NFTs.)
Code and data
All code is available at http://github.com/harangju/crafting-case-study. All data is publicly available through Axie’s GraphQL and Ronin APIs.
References
- Sky Mavis. (2022, January 20). 🔥 Axie Releasing 🔥 All Aboard the Lunacian Express! The Lunacian. https://axie.substack.com/p/lny2022
- Sky Mavis. (2022, July 14). 🏖️ Lunacian Summer: Breed Limited Edition Summer Skins! The Lunacian. https://axie.substack.com/p/summerskins
- Grow, A., Melanie, D., Pagnutti, J. Wardrip-Fruin, N., Mateas, M. (2017) Crafting in Games. Digital Humanities Quarterly, 11(4)
- Cook, D. (2021, December 12). Value chains – A method for creating and balancing faucet-and-drain game economies. Lost Garden. https://lostgarden.home.blog/2021/12/12/value-chains
- Kleiber, C., Kotz, S. (2003). Statistical size distributions in economics and actuarial sciences. Wiley.
- Eliazar, I. (2017). Lindy’s Law. Physica A: Statistical Mechanics and its Applications, 486, 797-805.